什么是信息熵？从存储单位到信息熵

我们都知道，计算机的存储单位有KB、MB、GB、TB等，换算起来，1TB=1024GB、1GB=1024MB、1MB=1024KB、1KB=1024B。1B我们称为一个字节，一个字节有8位，即1B=8bit。bit表示计算机的位，同时它也是信息熵的度量单位。

什么是信息熵?

信息是个很抽象的概念。人们常常说信息很多，或者信息较少，但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信息量。

直到1948年，香农提出了“信息熵”的概念，才解决了对信息的量化度量问题。信息熵这个词是C.E.香农从热力学中借用过来的。Shannon 借鉴了热力学的概念，把信息中排除了冗余后的平均信息量称为“信息熵”，并给出了计算信息熵的数学表达式。

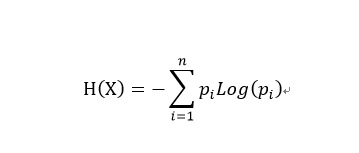
通俗的理解，当一个事物有多种可能发生的情况时，具体单个情况发生的不确定性叫做熵，而能够消除这种情况发生的不确定性的事物叫做信息。二者数量相等，意义相反，我们可以通过获取信息来消除不确定性(熵) 。能够消除不确定性的信息有三种类型：

1) 调整概率

2) 排除干扰

3) 确定情况

以商场抓奖活动为例，你的面前有四个颜色分别为红、黄、蓝、绿的小球，其中一个小球里面有大奖。如果四个小球获奖概率相等(都是1/4)，那么此时的信息熵最大;如果确定了红色小球里面有奖，那么此时的信息熵最小。

如果我们告诉客户，蓝色小球有一半的概率有奖，这就是调整概率，使得蓝色小球中奖的不确定性降低，其他小球中奖的不确定性增加;如果我们告诉客户，绿色小球肯定没有奖，这就是排除干扰，使得绿色小球没有了不确定性，其他小球获奖的不确定性也降低了;如果我们直接告诉客户红色小球里面有奖，这就是确定情况，使得消除了各个小球的不确定性。

定量看信息与信息熵

我们知道，当事物发生的不确定性越大，它的信息熵越大，反之，信息熵越小。但是我们如何量化信息呢，为何信息熵的还有单位(bit)?

弄清这个问题前，我们先看一下我们是如何定义其他常见的物理量(长度、质量、时间)的呢?

以长度为例，米是如何定义出来的，我们如何去量化一个物体的长度呢?答案是我们选择了参照物标准，我们规定了一个物体长度为1米，其他物体的长度就相当于多少倍参照物体的长度。比如一个物体的长度是参照物的长度的两倍，参照物长度1米，那么这个物体的长度就是2米。

与长度、质量、时间相同，信息熵也是一个物理量。把长度定义引申到信息熵，我们如果也定义一个参照事件的不确定性(信息熵)，只要看待测事件的不确定性(信息熵)相当于多少个参照事件的不确定性(信息熵)即可。

抛一枚硬币，有正、反两种等概率情况，这个事件所能产生的结果的信息熵我们规定为1bit，上文中4个小球抓奖，有四种等概率情况，这个事件所能产生的结果的信息熵相当于我们抛两次硬币所产生的结果，因此为2bit。不过要注意，如果是8个小球抓奖，有八种等概率情况，信息熵不是4bit，而是3bit(2^3=8)，因为八种等概率情况相当抛3次硬币所产生的结果，它们之间是指数关系。

到这里，我们就得到了信息熵的公式了，它的单位是bit。

本文来自：黑马程序员 大数据学院 cloud.itheima.com